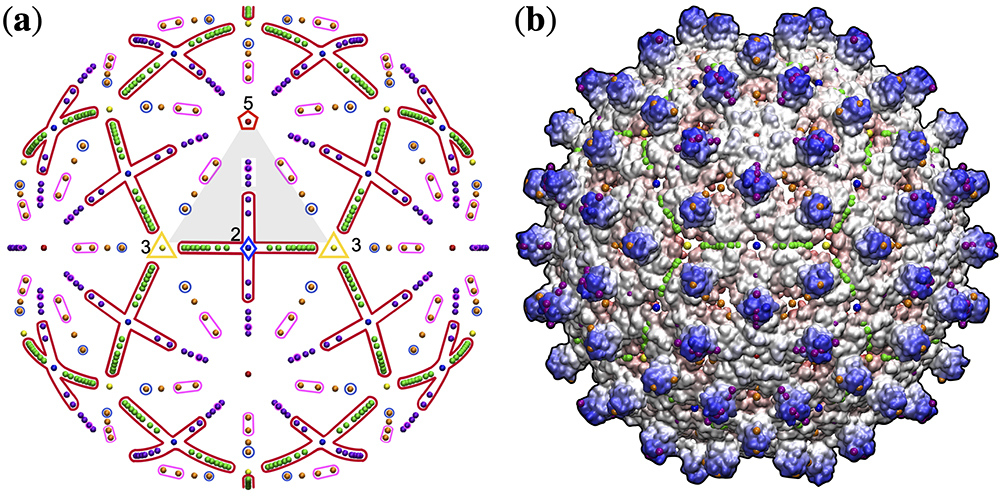
The last several years have highlighted the importance of understanding virus structures, assembly, and their potential mutations. In this talk, we will explore recently discovered empirical rules governing nearly all spherical (icosahedral) viruses ranging over 121 distinct virus types (genera). These rules emerge as a consequence of viral capsids adhering to geometric constraints of a radially extended form of icosahedral symmetry, referred to as point arrays, introduced by Keef and Twarock. While the physics governing these constraints is not yet clear, we are employing point arrays as a toolset to uncover new physical features in viral capsids. We have shown that nearly all spherical viruses place their protruding features on a common set of 21 locations within the icosahedral asymmetric unit.
These protrusions often have significant biological functions, aiding in stability and recognition by the host organism. We will show that these locations impose further constraints on the available internal arrangements of proteins and genetic material, which can be used to predict the genomic composition of viruses. Point arrays offer critical insights into the arrangements and structural modifications of viral capsid proteins, both inside and out, as well as helping us understand their evolutionary constraints and the biological engineering of viral structures, especially in cases where chemical modification should work, yet inexplicably fail. We will also show how these constraints explain several unexplained experimental results, including the immutable surface loops of bacteriophage MS2 and the non-quasi-equivalent flexibility of the HBV dimers. We will also discuss how using a physics based mindset lead to these results.














